Option Greeks. Real Options Analysis.

Choosing of assets for trading can take a long time, especially when it comes to options trading. Keeping this in mind, we’ve created the options screener that saves your time and helps find new trading ideas based on a simple principle – buying cheap options or selling expensive ones.
In this article we’ll cover the most memorable Option Greeks, so we’re going to look at delta, gamma, theta and vega. We’ll think about what the implications of these «Greeks» are but really we’re going to boil down to what Greek matters the most and how to apply them in different options trading strategies.
Contents
- Introduction to Option Greeks
- Delta option greek
- Gamma option greek
- Theta option greek
- Vega option greek
Introduction to Option Greeks
For each of these Greeks I can basically boil down each of them just to one word.
When we’re looking at delta we’re really looking at direction. There’s a lot of other things that delta can be used for but mainly we’re looking at directionality. If I’m bullish on a trade, if I’m bearish on a trade or if my whole portfolio is skewed to the downside or skewed to the upside that’s going to be delta. We’re going to be able to see where our directionality is and basically where our assumption lies by looking at delta.
When we’re looking at gamma we should know that it is related to delta. Gamma is considered basically the rate of change or the acceleration amount of delta. It shows us how much more you are going to make for each next dollar.
With theta the one word we need to know is time. Theta is the rate of decay of an options price so basically we’re thinking about time and how time value is either beneficial for us or if it’s going against us depending on whether we’re short options or long options.
With vega we’re really just focused on our volatility exposure and what that means from a buyer side and a seller side. Vega shows what the impact is on the option for a 1% change in volatility.
Delta Option Greek
When we’re looking at delta the basic definition is it’s a rate of change of an options price given a $1 increase in the underlying price. Calls have positive delta between 0 and 1, puts have negative delta between -1 and 0. So if the stock price moves up it’s good for calls whereas it has negative impact on puts. If the market moves down it will be good for put options.
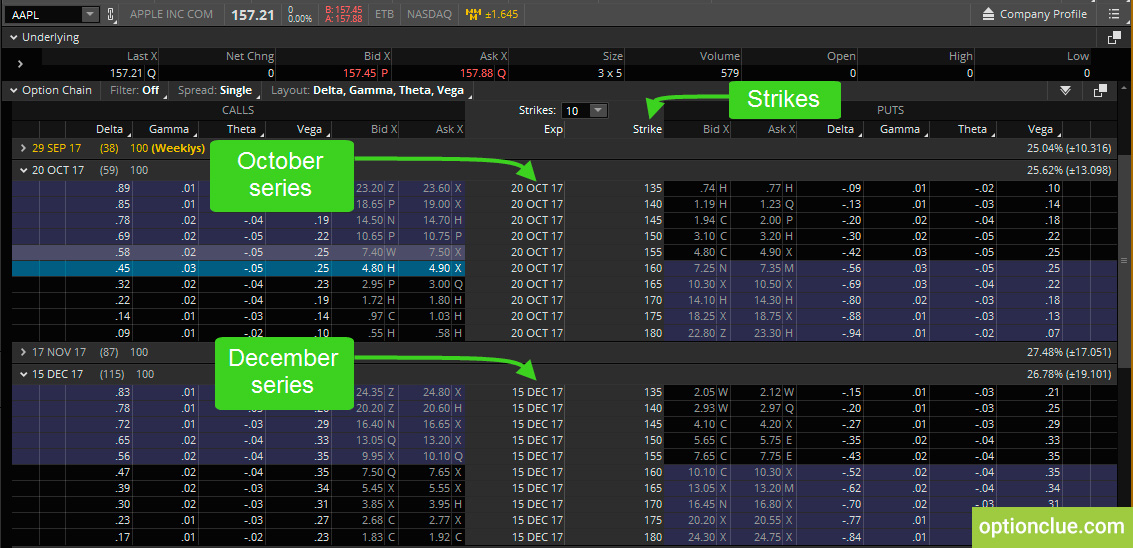
Let’s take some example from the thinkorswim trading platform. We look at the Apple stock which is trading at $157.20 (Figure 1).
We’ll look at two different option series, that is October and December expirations. October expiration has 59 days to go and December one has 115 days till expiration. We will take 2 different cycles to demonstrate the changes in this values (Figure 2).
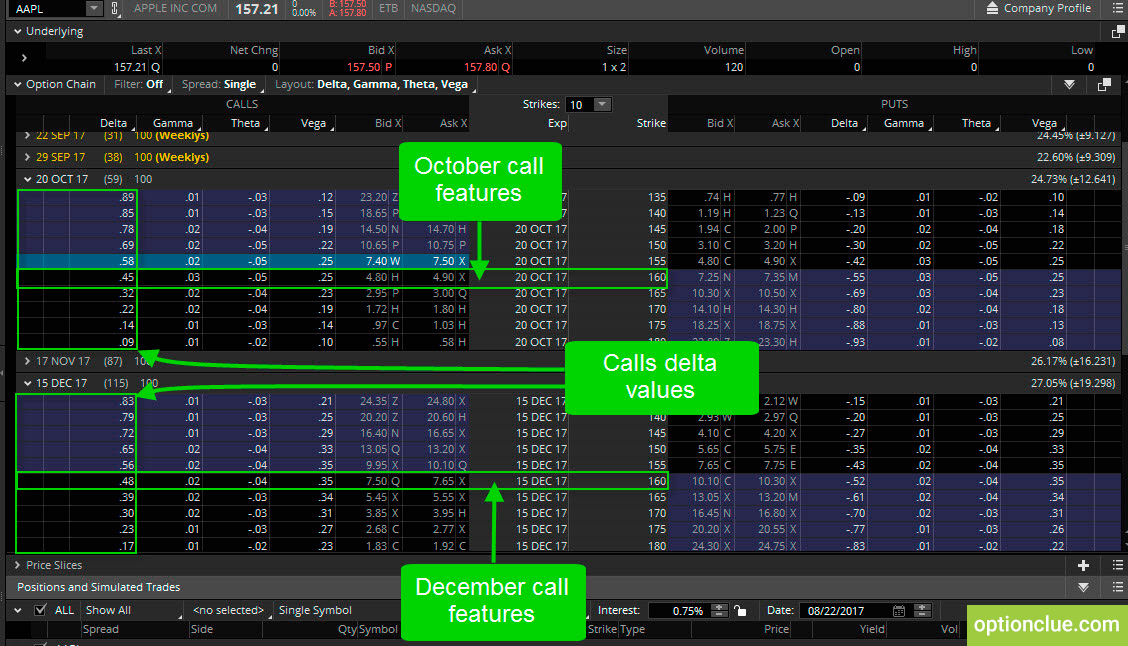
Figure 2. Calls. Delta change. Same strikes and different option series (thinkorswim trading platform)
For example, if I have a 160 call that is trading for $4.90 and I have 0.45 delta if there’s a $1 increase in the underlying price to $158.21 then the call price will increase to $5.35.
If we look at a 160 call in December expiration, you can see a bigger impact of the same movement of the underlying stock because there is more time left until expiration. If there’s a $1 increase in the underlying price to $158.21 then you’ll see that call price increases by $0.48. Although these options cost more than the options with October expiration, they can benefit more if the price gives the same move.
In both option series the more we move in-the-money with calls the delta is going to get deeper and deeper and basically higher and higher closer to 100 delta value. As we move further out-of-the-money with calls our delta is going to decrease below 45 and 48 and eventually we’ll have a delta of 0 if we get really far out-of-the-money and it’s not being traded at all.
If I have a higher probability of being in-the-money which would definitely be true for in-the-money options I’m going to have a higher delta and conversely if I’m looking out-of-the-money I’m going to have a lower probability of being in-the-money.
When we go to the put side of options, we can see that the delta value is negative (Figure 3).
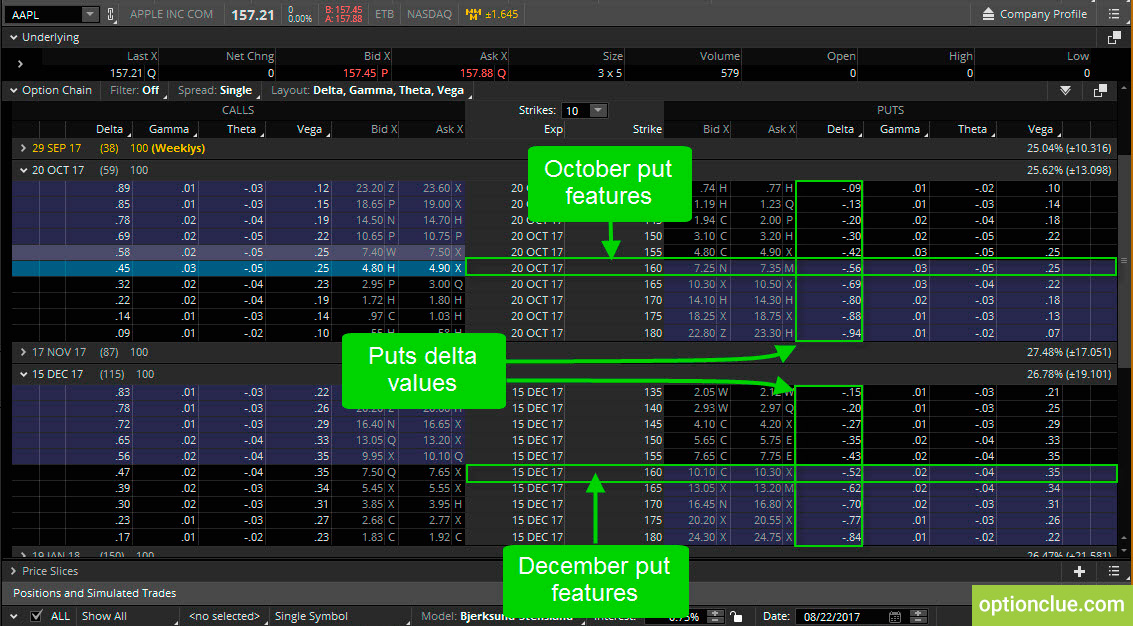
Figure 3. Puts. Delta change. Same strikes and different option series (thinkorswim trading platform)
We take the same 160 strikes both in October and December cycles. Despite delta is negative it doesn’t mean you’re going to lose money, it only indicates how much money you will make in case of $1 increase in the underlying price. So if you own the October 160 strike put and the stock rises by $1 to $158.21, the value of the option contract will decrease by $0.56 when it comes to December cycle this value will be $0.52. But, if Apple falls by $1 to $156.21 you will make money, in our case the sum is $0.56 and $0.52.
Usually we can use delta interchangeably when looking at the option and looking at that delta value and comparing it to the probability of being in-the-money.
We can also use it as a hedging tool. If we consider that options are the theoretical equivalent of 100 shares of stock if I own 100 shares of stock that would give me 100 delta because every share of stock gives me 1 delta.
If I have 100 long shares and I’m looking to hedge those long deltas from those 100 long shares what I can do is create a covered call, which gives us the ability to hedge our long exposure by selling a call against it.
If I sold a 30 delta call, it’s going to give me a negative delta. So, I instantly hedge my 100 delta down to a 70 delta because if I have long 100 deltas and I sell 30 deltas it gives me 70 deltas.
If I have a positive delta that would indicate that I’m bullish on the underlying or bullish on the market and if I have a negative delta that would indicate that I’m bearish on the market or that I’m a bear when it comes to where I want the market to go. Positive delta means I want the market to go up and negative delta means I want the underlying asset to go down.
Gamma Option Greek
Gamma is the rate of change of delta given a $1 move in the underlying price. Options with higher gamma are the most responsive to stock price changes in the underlying asset. It can be considered as the additional profit for the next dollar move.
Suppose I have a 160-call with October expiration and it has a delta value of 45 which means it’s definitely out-of-the-money because that delta value is less than 50 and I have a point of 3 gamma if the underlying price moves up one dollar (Figure 4).
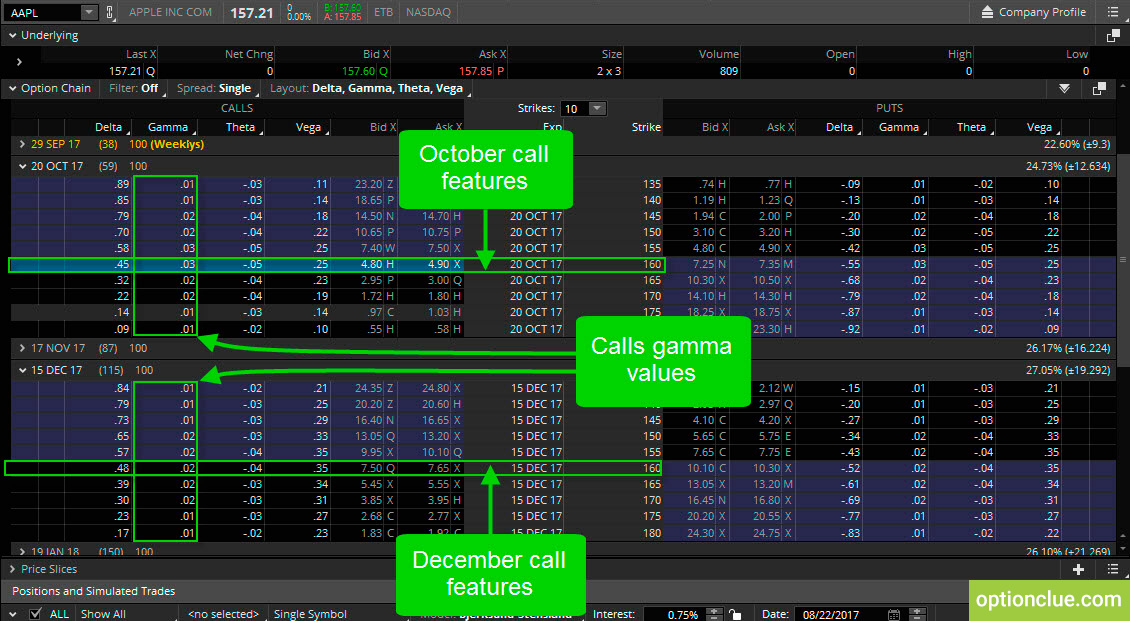
Figure 4. Calls. Gamma change. Same strikes and different option series (thinkorswim trading platform)
It means if Apple stock increases from the current price by $1 to $158.21 you’ll make $45. But if the stock price goes up increasing by another $1 to $159.21 you’ll make another $45 plus additional $3, that is $48 thanks to the gamma value.
As you can see, gamma accelerates our profits but it can also accelerate our losses depending on what side of the coin we are. So, if the stock price falls by $1 the cost of the option will decrease by $45 and the next dollar this value will be $48.
If we take the December cycle and the same option strike the gamma will be 2, it’s the lower value since we’re further from the expiration date. In this case, the additional sum we make or lose will be just $2 beginning from the second dollar price movement.
On the put side let’s look at 160-puts (October and December expiration cycles) (Figure 5).
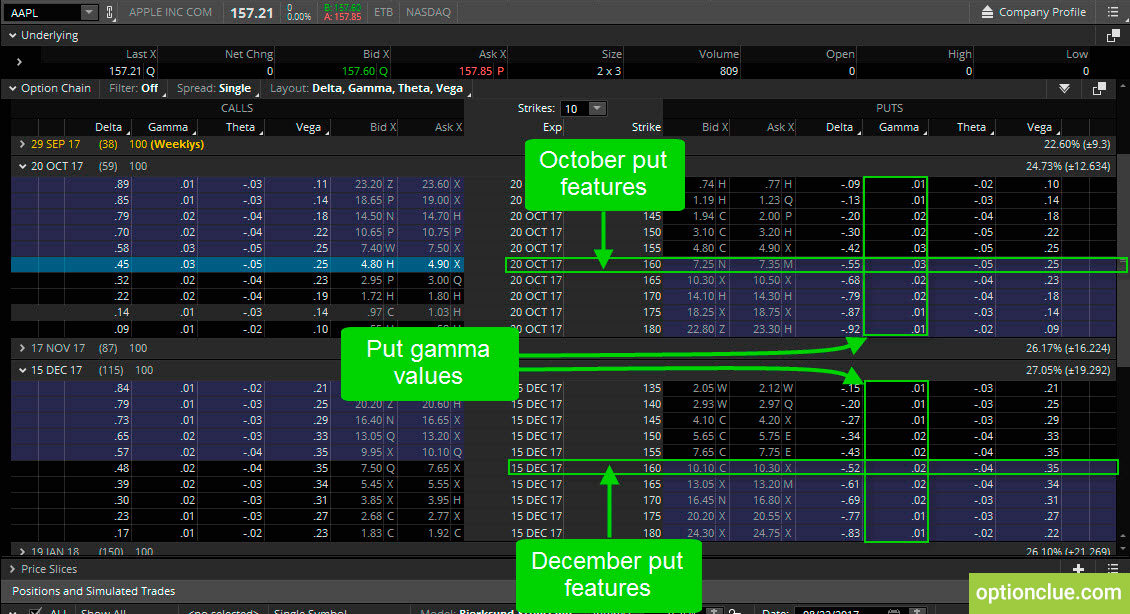
Figure 5. Puts. Gamma change. Same strikes and different option series (thinkorswim trading platform)
If Apple stock decreases from the current price by $1 to $156.21 you’ll make $55 in October and $52 in December. But if the stock price goes down increasing by another $1 to $155.21 you’ll make another $55 plus additional $3, that is $58 for October expiration and $52 plus additional $2, that is $54 for December expiration.
In case the stock price goes up the same distance, you will lose this amount of money due to the delta and gamma values.
One thing to realize is that gamma increases at expiration. When I’m looking at a gamma of about 3 or 0.03 it’s a pretty low value, but if I’m closer to expiration where there’s only five or six days left I might see a gamma of 10 or maybe 15 where I’m going to see my delta rapidly change which can either be good or bad depending on my situation.
When we’re looking at gamma it’s going to be a positive thing for buyers. So if I were to buy a naked option gamma would actually be on my side because if the underlying continually goes for me and it continually moves my strike deeper in-the-money I’m going to make more value for every extra dollar that the option goes in the money or every extra dollar that the underlying increases that can compound our profit potential.
For that reason, it’s going to be a bad thing for sellers that is why we tend to roll our positions. So, if I have a position that expires this week I’ll look to roll it to a next expiration cycle because the more time we have on our side the lower the gamma is going to be.
If I’m selling stock options I don’t want my option prices to whip around.
When we’re looking at gamma if I were to buy naked options or buy, for example, a diagonal spread, I’m going to have gamma on my side when it goes deeper and deeper in-the-money and make the option profitable for me.
When we’re looking at sellers it’s the opposite. If I’m selling an option gamma is going to be something that could hurt me over time because if my option moves in-the-money which is bad for a seller, the deeper it moves in-the-money, the more losses will accelerate.
Theta Option Greek
Let’s go on to the next Greek theta. Theta shows the amount the price of calls and puts will decrease as these contracts approach the expiration date. So, theta is the best friend for option sellers since it provides more profit potential closer to expiration.
When we’re looking at theta from that perspective the first thing I’d like to note is that if I’m a seller of an option I want the option to decrease in price. If I’m selling an option I want the option to decay with every day that passes to allow me to buy it back at the lower price for profit.
If I’m a seller theta is going to be beneficial to me and if I’m a buyer it’s going to be the opposite because if I bought this call I need the underlying to move up in price because when I buy a call I want to be able to buy those shares at a discount which is exactly what would happen if the stock price continued to rise. But if it doesn’t rise and nothing happens but time passes, then my option is going to be less worth over time. So, theta is going to have a negative impact in this case.
One interesting thing is that when we’re looking at theta how it actually decreases for out-of-the-money options at expiration because as we get closer to expiration they become pretty much worthless. So there’s not much else to decay if an option is only worth two or three cents and there’s five days left it can’t really decay any further than that until it hits zero.
With at-the-money options that definitely hold their value the longest if I have five days left until expiration I probably could see an option still worth maybe twenty or thirty cents so it still is going to have that theta and it’s going to accelerate because at expiration it has to be worth zero.
Suppose I have a 160-call for $4.90 with October expiration (59 days left) and 160-call for $7.65 with December expiration (115 days left). Theta is negative for all options in every expiration cycle since it represents the options decay (Figure 6).
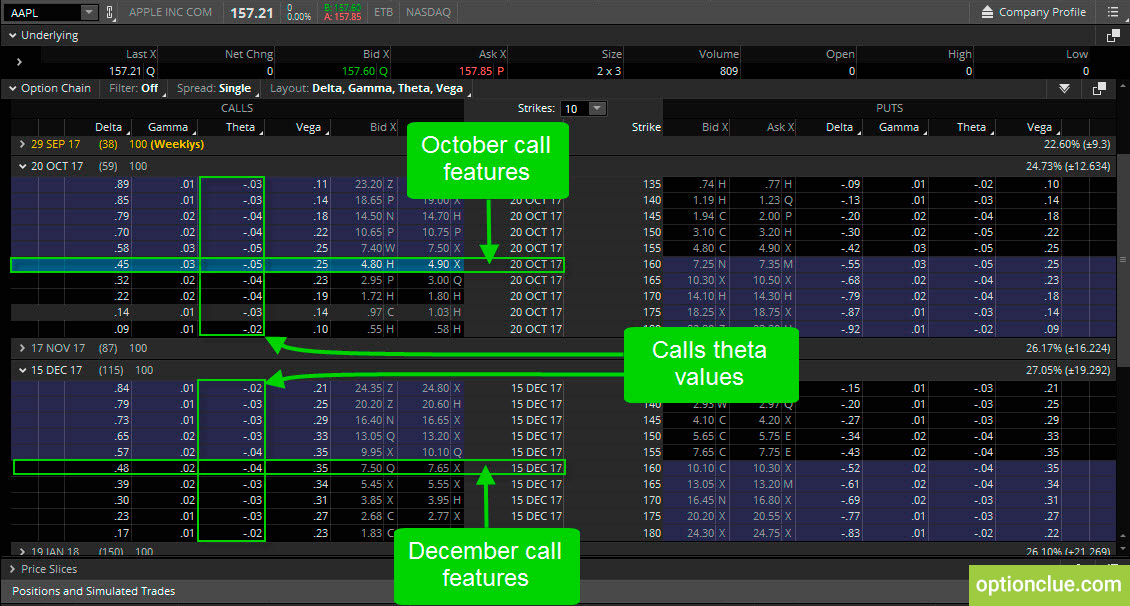
Figure 6. Calls. Theta change. Same strikes and different option series (thinkorswim trading platform)
Theta has really small value because the option has a lot of value itself. As we get closer to expiration, theta really increases.
You can see October 160 call option has a negative theta of .05 and at the same time December 160 call has a negative theta of .04 that means that we are losing $5 and $4 per day respectively no matter what happens to the underlying stock.
So time decay aspect is very important since it helps understand whether you can make money when trading any particular option or not and how it affects the option price when you approach the expiration date.
Vega Option Greek
Let’s get to our last Greek which is vega. Vega is just our rate of change of an options price given for every 1% change in implied volatility. Vega affects only the time value of an option’s price and has no impact on the intrinsic value.
Suppose I have 160-call option trading for $4.90, which has 25 vega value (Figure 7). If implied volatility increases by 1% in that underlying stock, then I’ll see my call increased by $0.25. So my call’s price will go from $4.90 to $5.15 which gives me that 25 vega value.
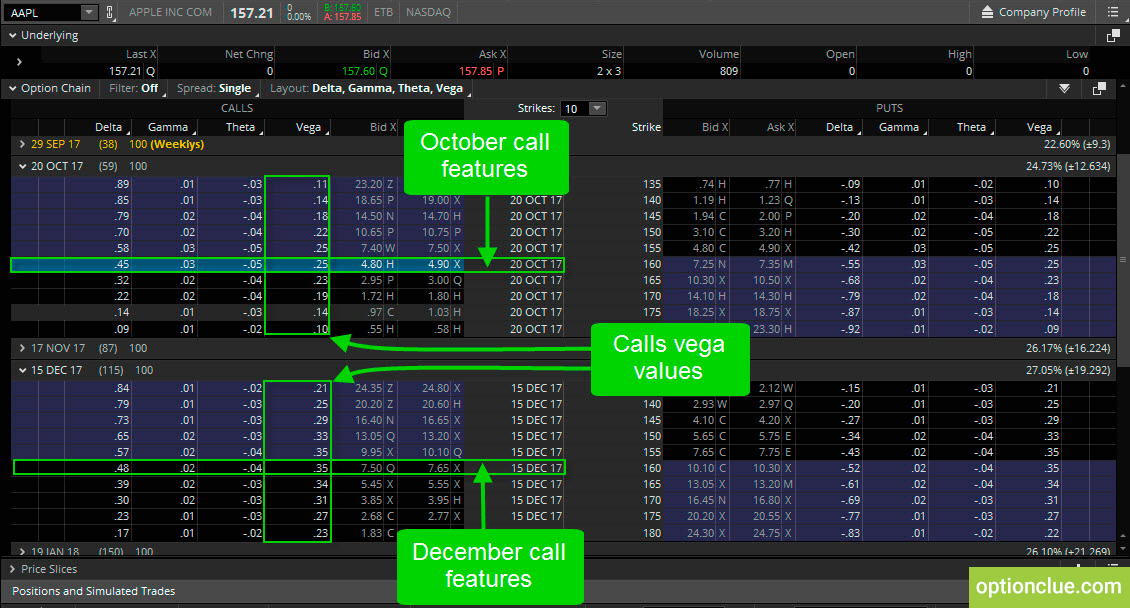
Figure 7. Calls. Vega change. Same strikes and different option series (thinkorswim trading platform)
Let’s take one of the top option stocks, the Apple stock chart and look at how it really works (Figure 8).
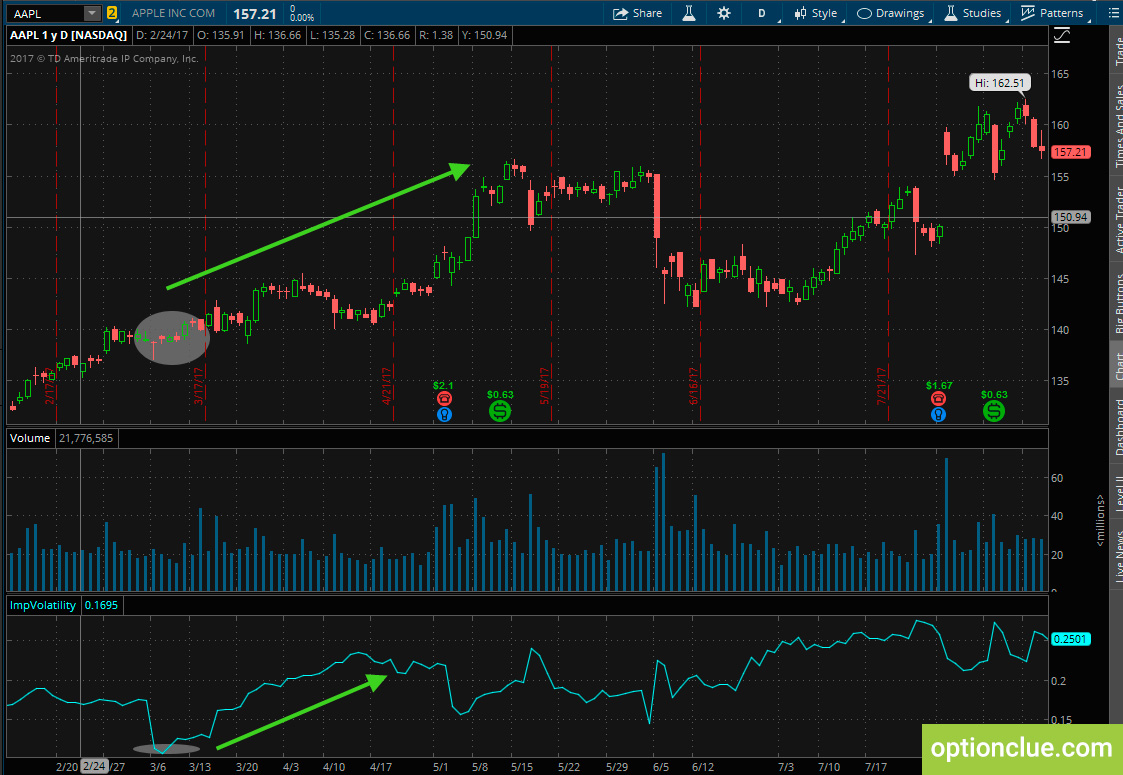
Figure 8. Implied Volatility application when analyzing the stock chart (thinkorswim trading platform)
As you can see on the chart Apple was traded about $140 in a pretty narrow price range one day and the implied volatility was too small (about 0.1). Taking into account this fact some traders expected the stock to be more volatile in the near future and it was the chance for them to enter the market in the condition of low volatility. The price movement in the next several weeks proves that after a big jump in implied volatility (to 0.25) the stock price increases by $17 that enabled making profit from both the vega value and underlying asset increase.
Understanding and proper application of «Greeks» enables you to have best option trades today.